Doing the Test
Now lets actually get into the mechanics of doing the hypothesis test.
These are the summary statistics that will be needed to perform a hypothesis test.

We will be using the top 3 rows out of the bottom 4 to compute the test statistic (this test uses a t-ratio).
The t-ratio is determined by this equation:
(x̄A-x̄N-(µA-µN))/SE(x̄A-x̄N).
x̄A-x̄N represents the observed difference in means of the data.
µA-µN represents what we are hypothesizing to be the true difference in the actually means of the population.
We subtract µA-µN from x̄A-x̄N because it shows the difference from what we'd expect. It's this difference that we want to test to see if it is significant.
So why do we divide by SE(x̄A-x̄N)? Well, different sets of data from different population will have different means and will vary differently. However, the test being performed uses a single model (or equation, if you will) to determine if a difference is significant. The problem is, while the equation might be good for one scale, it would be terrible for another. Dividing by SE(x̄A-x̄N) "standardizes" the data onto one common scale, allowing the test to use it's "one-size-fits-all" method.
We've know that the observed difference in the data is (x̄A-x̄N) 4.7333333.... If we assume the null hypothesis to be true, then we are assuming that there is no difference between the actual population means (We are assuming that µA-µN=0. Which is why that alternative way of writing the null hypothesis is used). We can also calculate SE(x̄A-x̄N) to be about 1.04.
This makes the t-ratio (4.7333333....-0)/~1.04≈4.54.
We then use the model this test uses (a t-model) to turn the t-ratio of about 4.54 into a P-value. A P-value is the probability of getting the difference we saw (or a larger difference) in the data if there is no actual difference in the populations.
The area under the curve (where the arrow is pointing; to the right of the bar) shows the P-value. The area is very small. So small, in fact, that you can't even see it.
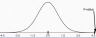
As it turns out the P-value is about .015%, which is extremely miniscule.
Conclusion
The P-value is very small. The probability of seeing a difference of 4.73333... between the means of the data is .015% if the null hypothesis (which is that there is no difference between the true means) is true. I find this probability too small, and reject the null hypothesis (a fancy way of saying: "this probability is so small that I don't think that the null hypothesis is actually correct) in favor of the alternative. These results lead me to believe that advertising your sequences on the OS forums does increase the amount of views that they get.
Well, if you're reading this text, then you have most likely just read through (or at least skimmed or looked at the highlighted sections) this giant wall of text that is me trying to explain a statistical process to you. Thank you for not tl;dr-ing this (I put a lot of effort into it). If you have any questions regarding this inference, please don't hesitate to ask! I'd be happy to clear up any confusions.
Now lets actually get into the mechanics of doing the hypothesis test.
These are the summary statistics that will be needed to perform a hypothesis test.
We will be using the top 3 rows out of the bottom 4 to compute the test statistic (this test uses a t-ratio).
The t-ratio is determined by this equation:
(x̄A-x̄N-(µA-µN))/SE(x̄A-x̄N).
x̄A-x̄N represents the observed difference in means of the data.
µA-µN represents what we are hypothesizing to be the true difference in the actually means of the population.
We subtract µA-µN from x̄A-x̄N because it shows the difference from what we'd expect. It's this difference that we want to test to see if it is significant.
So why do we divide by SE(x̄A-x̄N)? Well, different sets of data from different population will have different means and will vary differently. However, the test being performed uses a single model (or equation, if you will) to determine if a difference is significant. The problem is, while the equation might be good for one scale, it would be terrible for another. Dividing by SE(x̄A-x̄N) "standardizes" the data onto one common scale, allowing the test to use it's "one-size-fits-all" method.
We've know that the observed difference in the data is (x̄A-x̄N) 4.7333333.... If we assume the null hypothesis to be true, then we are assuming that there is no difference between the actual population means (We are assuming that µA-µN=0. Which is why that alternative way of writing the null hypothesis is used). We can also calculate SE(x̄A-x̄N) to be about 1.04.
This makes the t-ratio (4.7333333....-0)/~1.04≈4.54.
We then use the model this test uses (a t-model) to turn the t-ratio of about 4.54 into a P-value. A P-value is the probability of getting the difference we saw (or a larger difference) in the data if there is no actual difference in the populations.
The area under the curve (where the arrow is pointing; to the right of the bar) shows the P-value. The area is very small. So small, in fact, that you can't even see it.
As it turns out the P-value is about .015%, which is extremely miniscule.
Conclusion
The P-value is very small. The probability of seeing a difference of 4.73333... between the means of the data is .015% if the null hypothesis (which is that there is no difference between the true means) is true. I find this probability too small, and reject the null hypothesis (a fancy way of saying: "this probability is so small that I don't think that the null hypothesis is actually correct) in favor of the alternative. These results lead me to believe that advertising your sequences on the OS forums does increase the amount of views that they get.
Well, if you're reading this text, then you have most likely just read through (or at least skimmed or looked at the highlighted sections) this giant wall of text that is me trying to explain a statistical process to you. Thank you for not tl;dr-ing this (I put a lot of effort into it). If you have any questions regarding this inference, please don't hesitate to ask! I'd be happy to clear up any confusions.